What is a collision?

So far, we’ve seen how to load up a hash table with data that very conveniently didn’t cause any problems. Needless to say, that was unrealistic. Sometimes, if you apply a hash function to two different keys, it generates same index number for both. But both items can’t go in the same place. This is known as a collision.

Collision resolution

Below you can see a hash table being populated with a different set of data that causes a few collisions. The hash function is the same as we saw previously, namely:

Sum of ASCII codes Mod Size of array

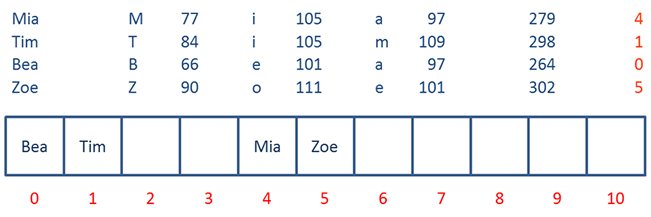
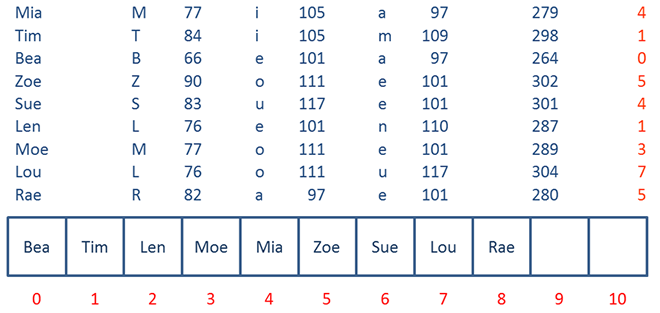
When the hash table is loaded first with Mia, then Tim, then Bea then Zoe, there are no problems, each item can be placed at its calculated address.

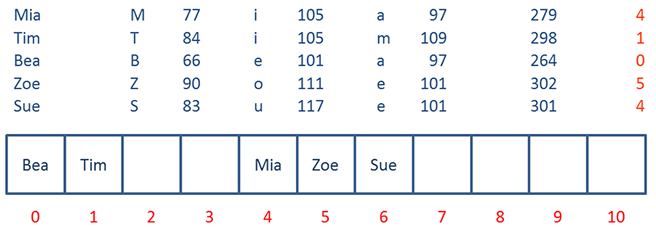
But Sue causes a problem.  The calculated address for Sue is already occupied by Mia.  The resolve this collision, Sue is placed into the next available slot in the hash table.

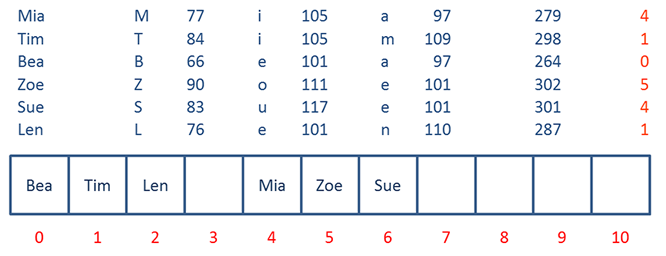
The calculated position for Len is also occupied (by Tim), so Len is placed in the next available slot.

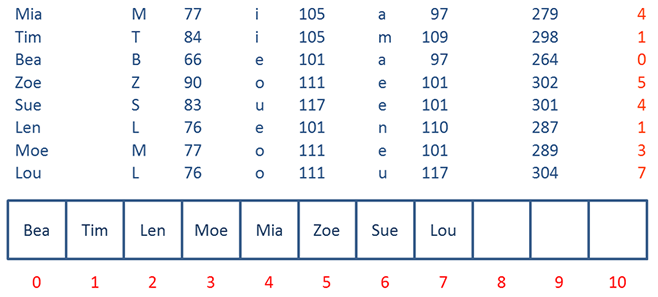
When the hash function is applied to Moe and Lou, they do not cause collisions so Moe and Lou can be put into their calculated positions.

Rae however cannot be placed at address 5, so is placed in the next available slot, address 8.

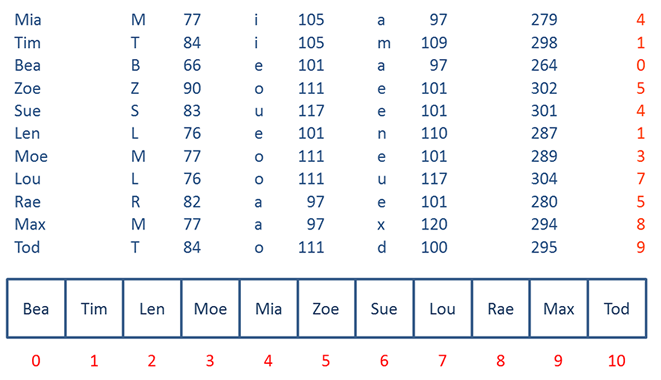
When the last two items are added, they too have now been displaced.

Open addressing

Resolving collisions by placing an item somewhere other than their calculated address is called open addressing, because every location is open to any item. Open addressing can use a variety of techniques to decide where to place an item that doesn’t go where it should.

This particular open addressing technique is called linear probing. If the calculated address is occupied, then a linear search is used to find the next available slot.

If linear probing gets to the end of the array and it still can’t find a free space, it might cycle around to the beginning of the array and continue searching from there.

To look up an item in a hash table that has been populated with linear probing, the hashing function is applied again, but if there have been collisions, and some items are not in their in calculated positions, then finding the item will also involve some linear probing – that is, a linear search.

Load factor

The more items there are in the hash table, the more likely you are to get collisions when you insert even more data. One way to deal with this is to make the hash table bigger than needed for the total amount of data you’re expecting, perhaps such that only 70% of the hash table is ever occupied. The ratio between the number of items stored, and the size of the array, is known as the load factor. If the hash table is implemented as a resizeable, dynamic data structure, it could be made to increase in size automatically when the load factor reaches a certain threshold.

In an ideal world, every item will be stored in the hash table according to its calculated index. In this best case scenario then, the time taken to find any particular item is always the same. But you can imagine a worst case scenario too. Depending on the nature of the data used to calculate the index values, and depending on the appropriateness of the hash algorithm, some items may require a linear search of the whole list in order to be found.

As long as the load factor is reasonable low, open addressing with linear probing should work reasonable well.

Probing techniques

When resolving collisions, if the calculated address is occupied, linear probing involves trying the next place along, and if necessary the next then the next, and so on, until an empty space is eventually found. But this can result in what is known as primary clustering. In other words keys might bunch together inside the array while large portions of the array remain unoccupied. There are however alternatives to linear probing which can help to avoid clustering .

Rather than simply scanning along for the next available slot, collision resolution may involve looking at every third slot along until a free space is found – the so called +3 rehash.

Quadratic probing will square the number of failed attempts when deciding how far along from the point of the original collision to look next. Each time another failed attempt is made, the distance from the original point of collision grows rapidly.

Double hashing applies a second hash function to the key when a collision occurs. The result of the second hash function gives the number of positions along from the point of the original collision to try next.

Closed addressing

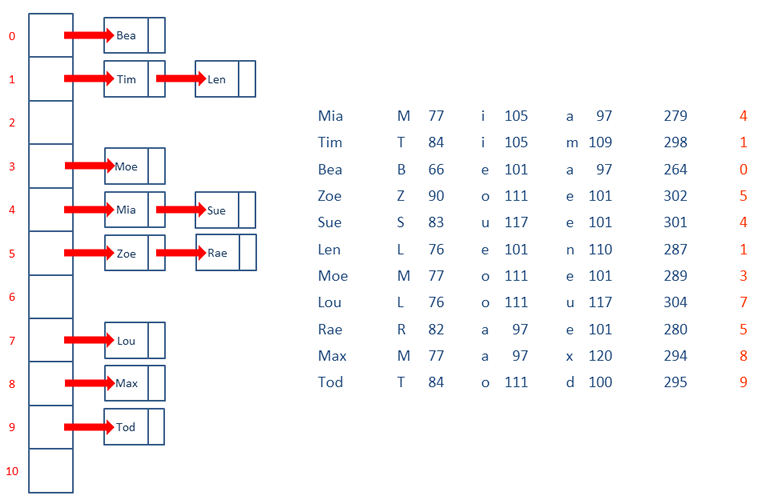
Another way to deal with collisions is known as chaining, sometimes referred to as closed addressing. Closed addressing involves chaining together items that have collided in a linked list (or some other suitable data structure).  This means that each element of the array might contain a pointer to a linked list.

Here is the same data we saw before loaded into a hash table that resolves collisions with closed addressing.

With the chaining method of conflict resolution, you can see there are a greater proportion of items in the correct place, so the lookup is quicker than if you had used linear probing.

To search this hash table, you can calculate the index as before to locate the correct element, then use a standard linked list traversal to find what you are looking for.

Of course traversing a linked list also comes at a cost, if the load factor is low, it may actually be more efficient to use open addressing.

Objectives of the hash function

If you know all of the keys in advance, then it’s theoretically possible to come up with a perfect hash function, one that will produce a unique index for each and every data item. In fact, if you know the data in advance, you could probably come up with a perfect hash function that uses all of the available spaces in the array.  More often than not, you will not know the precise nature of the data in advance and will therefore need a more flexible hash table, so when choosing, or writing a new hash function, there are some objectives of the hash function to bear in mind.

• It should minimise collisions, so less time is spent on collision resolution, and ultimately data retrieval will be quicker.
• Ideally, it should give you a uniform distribution of hash values, and therefore the data will be spread across the has table as uniformly as possible.
• It should be easy to calculate.
• It should include a suitable method of resolving any collisions that do occur