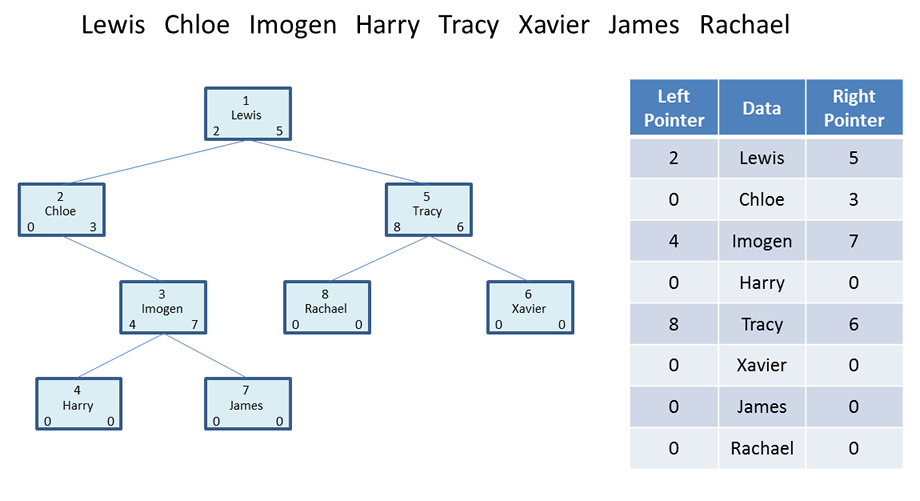
To implement a binary tree you can use 3 array variables. One array to hold the data items, a second array to hold a set of left pointers and a third array to hold a set of right pointers.
In the example below, data has been loaded into the binary tree in the order: Lewis, Chloe, Imogen, Harry, Tracy, Xavier, James and Rachael.
How the tree is constructed
The tree is constructed as the data arrives.
Lewis arrives first and becomes the root node. The left and right pointers of Lewis are both set to 0.
When Chloe arrives, Chloe is placed to the left of Lewis, because Chloe is smaller than Lewis, alphabetically speaking. Because Chloe has been placed to the left of Lewis and is data item 2, the left pointer of Lewis is set to 2.
When Imogen arrives, Imogen should be placed to the left of Lewis, because Imogen is smaller than Lewis, alphabetically speaking, but this position is occupied, so the left branch is followed down to Chloe. Then Imogen is placed to the right of Chloe, because Imogen is larger than Chloe, alphabetically speaking. Because Imogen has been placed to the right of Chloe and is data item 3, the right pointer of Chloe is set to 3.
When Harry arrives, Harry should be placed to the left of Lewis, because Harry is smaller than Lewis, alphabetically speaking, but this position is occupied, so the left branch is followed down to Chloe. Harry should be placed to the right of Chloe, because Harry is larger than Chloe, alphabetically speaking, but this position is occupied, so the right branch is followed down to Imogen. Then Harry is placed to the left of Imogen, because Harry is smaller than Imogen, alphabetically speaking. Because Harry has been placed to the left of Imogen and is data item 4, the left pointer of Imogen is set to 4.
When Tracy arrives, Tracy is placed to the right of Lewis, because Tracy is larger than Lewis, alphabetically speaking. Because Tracy has been placed to the right of Lewis and is data item 5, the right pointer of Harry is set to 5.
When Xavier arrives, Xavier should be placed to the right of Lewis, because Xavier is larger than Lewis, alphabetically speaking, but this position is occupied, so the right branch is followed down to Tracy. Then Xavier is placed to the right of Tracy, because Xavier is larger than Tracy, alphabetically speaking. Because Xavier has been placed to the right of Tracy and is data item 6, the right pointer of Tracy is set to 6.
When James arrives, James should be placed to the left of Lewis, because James is smaller than Lewis, alphabetically speaking, but this position is occupied, so the left branch is followed down to Chloe. James should be placed to the right of Chloe, because James is larger than Chloe, alphabetically speaking, but this position is occupied, so the right branch is followed down to Imogen. Then James is placed to the right of Imogen, because James is larger than Imogen, alphabetically speaking. Because James has been placed to the right of Imogen and is data item 7, the right pointer of Imogen is set to 7.
When Rachael arrives, Rachael should be placed to the right of Lewis, because Rachael is larger than Lewis, alphabetically speaking, but this position is occupied, so the right branch is followed down to Tracy. Then Rachael is placed to the left of Tracy, because Rachael is smaller than Tracy, alphabetically speaking. Because Rachael has been placed to the left of Tracy and is data item 8, the left pointer of Tracy is set to 8.
Iterative pseudocode
The pseudocode below takes an iterative approach to building a binary tree. The variable iPosition is used to populate the Data array unconditionally. iPosition is incremented each time any item is added.
The very first item added is a special case, it is the root node and is therefore handled outside of the main loop. Its left and right pointers are both set to 0 to begin with.
The value of ptr is also set to 1 before the main loop starts. The variable ptr may then be repeatedly reassigned inside the main loop in order to follow a chain of pointers, which is effectively following the appropriate branches of the tree until a vacant position for the new node is found.
When a new item other than the root arrives, it is compared with data item 1, namely the root. If the new item is larger than the root, a test is made to see of the right pointer of the root is 0, in which case the new item can be placed to the right of the root; ptr is then set to 0 which is the exit condition of the loop. If the right pointer of the root is not 0, ptr is reassigned to be the value of the root’s right pointer. This means that in the next iteration, the new value is being compared with the right hand child of the root.
ptr = 1
iPosition = iPosition + 1
Data(iPosition) = NewData
If iPosition = 1 Then
Left_Pointer(iPosition) = 0
Right_Pointer(iPosition) = 0
Else
Do Until ptr = 0
If NewData > Data(ptr) Then
If Right_Pointer(ptr) = 0 Then
Right_Pointer(ptr) = iPosition
ptr = 0
Else
ptr = Right_Pointer(ptr)
End If
ElseIf NewData < Data(ptr) Then
If Left_Pointer(ptr) = 0 Then
Left_Pointer(ptr) = iPosition
ptr = 0
Else
ptr = Left_Pointer(ptr)
End If
End If
Loop
End If
Recursive algorithm to construct a binary tree
Let’s think through the process for adding another item to an existing tree. For example we want to add Beatrix the to tree above. First we compare the new value with the value of the root, Lewis, and decide to place Beatrix somewhere to the left of Lewis.
if newvalue < thisnode
Now we check to see if we can attach Beatrix directly to Lewis, making her child of Lewis.
if thisnode has no left child
insert new node here
In this example, Lewis’s immediate left is already occupied by Chloe, so we cannot place Beatrix here.
Now comes the clever bit. Let’s ask the same questions of Chloe that we asked about Lewis. We find that Beatrix should be placed to the left of Chloe.
If we were unable to place Beatrix to the left of Chloe, because the position was already occupied, we would repeat the process yet again.
Here is the complete algorithm, which you can see is a recursive approach:
if new value < this node
if this node has no left child
insert new node here
else
handle the left child with the same algorithm
end if
elseif new value > this node
if this node has no right child
insert new node here
else
handle the right child with the same algorithm
end if
end if
Recursive pseudocode
The following pseudocode program Insert_Node, creates a binary tree. You are advised to code up this algorithm and step through it carefully to see what is going on.
iPostion = 1 ‘Actual position of DataItem in data array
root = 1 ‘The current ‘root’ node
Sub Insert_Node(root As Integer, DataItem As String)
‘create the root node
If iPosition = 1 Then
Data[1] = DataItem
Left_Pointer[1] = 0
Right_Pointer[1] = 0
iPosition = 2 ‘ready for next item
Exit Sub
End If
‘left hand sub-tree search
If DataItem < Data[root] Then
If Left_Pointer[root] = 0 Then
‘insert new terminal node here
Data[iPosition] = DataItem
Left_Pointer[iPosition] = 0
Right_Pointer[iPosition] = 0
‘update root pointer
Left_Pointer[root] = iPosition
iPosition = iPosition + 1
Else
Call Insert_Node(Left_Pointer[root], Data) ‘this is where the root becomes another root
End If
End If
‘Right hand sub-tree search
If Data > Data[root] Then
If Right_Pointer[root] = 0 Then
‘insert new terminal node here
Data[iPosition] = Data
Left_Pointer[iPosition] = 0
Right_Pointer[iPosition] = 0
‘update root pointer
Right_Pointer[root] = iPosition
iPosition = iPosition + 1
Else
Call Insert_Node(Right_Pointer[root], Data)
End If
End If
End Sub
Explanation
Consdier what happens when this program is called with the following sequence of input data:
Larry, Charles, Albert…
When Larry is added at the very start, this should become the root node, so the value of 1 is passed into the procedure as the root node. Only the first IF block is executed and the data is added to postion 1 in the data array. The value of iPosition is then incremented so the data array is ready for the next data item.
When Charles is added, a check is made to see if Charles should be added to the left hand subtree by asking is the data value is less than that at position 1 of the data array (which it is).
If DataItem < Data[root] Then
The program then checks to see of the current left pointer is 0, in other words, if there is a vacant position to the left of the root node.
If Left_Pointer[root] = 0 Then
Because it is 0, Charles data is added to data array and the left and right pointers of this data item, Charles at iPosition = 2, are set to zero, because Charles has no child nodes yet.
Left_Pointer[iPosition] = 0
Right_Pointer(iPosition] = 0
The left pointer of the root, namely Larry is also updated to point to the second data item and the value of iPosition is incremented again in readiness for the next item.
Left_Pointer[root] = iPosition
When Albert is inserted, which is less than Larry, the left subtree is searched again. This is where it gets interesting. A check is made to see if the left pointer of the root is occupied
If Left_Pointer[root] = 0 Then
and because it is occupied, Insert_Node calls itself recursively with the command Call
Insert_Node(Left_Pointer[root], Data)
At this stage the current value of the root’s left pointer is 2, representing the Charles node. Charles therefore becomes the new root.
The program can now repeat the process, working from the newly defined ‘root’.