Traversing a binary tree is sometimes referred to as ‘walking the tree’.
Traversal of a binary tree provides a systematic way of listing all of the data in the tree. There are three ways this can be done:
- Pre-order traversal
- In-order traversal
- Post-order traversal
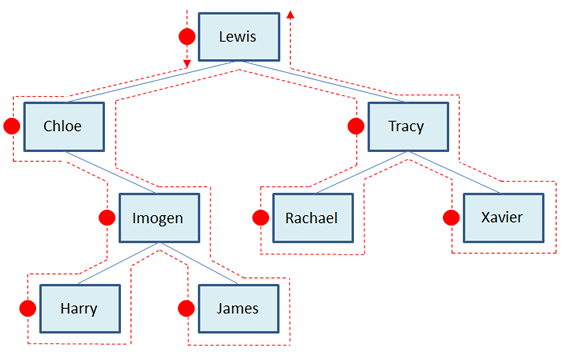
Pre-order traversal
An easy way to work out the data order produced by a pre-order traversal is to place a dot on the left hand side of each node as shown above. Then starting from the left hand side of the root, join the dots.
In effect, you are exploring the left sub-tree of the root first. Also, if you think of each node as if it were the root, you are exploring each node’s left sub-tree first.
Simple algorithm for pre-order traversal:
- Visit root
- Traverse left sub-tree
- Traverse right sub-tree
Pseudocode for pre-order traversal
PREORDER_TRAVERSE(tree)
Visit root of tree
PREORDER-TRAVERSE(left subtree)
PREORDER-TRAVERSE(right subtree)
By thinking of each node of the tree as if it were the root of another sub-tree, we can write a very simple recursive procedure to traverse the tree.
A more explicit version of this pseudocode is shown below. This is closer to an implementation.
PreOrder_Traverse(p)
OUTPUT Data(p)
IF Left_Pointer(p) <> 0 THEN
CALL PreOrder_Traverse(Left_Pointer(p))
END IF
IF Right_Pointer(p) <> 0 THEN
CALL PreOrder_Traverse(Right_Pointer(p))
END IF
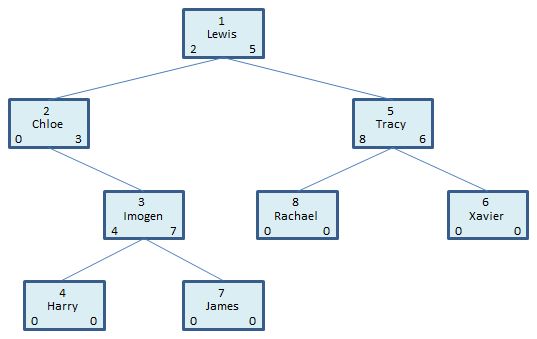
To understand this pseudocode, we need to remind ourselves of the system of pointers.
When the procedure is first called, it is passed the location of the first data item, namely Lewis at location 1, this is the root of the whole tree and can be output immediately. Then the procedure calls itself, passing in the left pointer of the root, namely Chloe at location 2. Chloe is now the new root and can be output. Because Chloe’s left pointer is 0, this means that there is no sub-tree to the left of Chloe to explore, so the procedure calls itself passing in Chloe’s right pointer. Imogen is now the new root, and this sub-tree is explored in the same way.
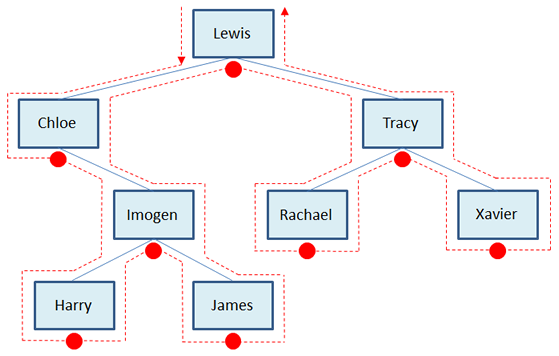
In order traversal
An easy way to work out the data order produced by in-order traversal is to place a dot below each node as shown above. Then starting from the left hand side of the root, join the dots.
The visitation order for an in-order traversal is left sub-tree, root, right sub-tree. This type of traversal will list the data in ascending alphabetical order (or numeric order if it is numeric data).
Simple algorithm for in-order traversal:
- Traverse left sub-tree
- Visit root
- Traverse right sub-tree
Pseudocode for in-order traversal:
INORDER_TRAVERSE(tree)
INORDER-TRAVERSE(left subtree)
Visit root of tree
INORDER-TRAVERSE(right subtree)
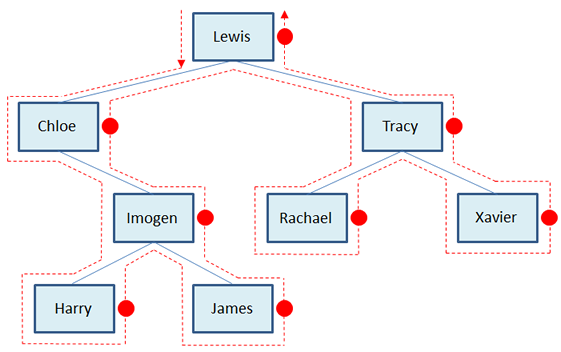
Post-order traversal
An easy way to work out the data order produced by post-order traversal is to place a dot on the right hand side of each node as shown above. Then starting from the left hand side of the root, join the dots.
The visitation order for post-order traversal is left sub-tree, right sub-tree, root. This type of traversal can be used to produce reverse polish notation from an expression tree.
Simple algorithm for post-order traversal:
- Traverse left sub-tree
- Traverse right sub-tree
- Visit root
Pseudocode for in-order traversal:
POSTORDER_TRAVERSE(tree)
POSTORDER-TRAVERSE(left subtree)
POSTORDER-TRAVERSE(right subtree)
Visit root of tree