Uses of graphs
The graph data structure has a great many applications in computer science, almost invariably to model different types of network. Travel routes such as road links, shipping lanes, or aircraft flight paths can be represented, including information about distances, speed limits, wind speed, fuel requirements, or just about anything of relevance. But it doesn’t stop there: A search engine might model the links between web pages on the Internet using graphs; The routing of data packets during transmission on a computer network can be represented by a graph; The connections between people and groups in social networks; The speed and pressure of liquids flowing inside pipes; Finding the quickest time to complete a project that includes several interdependent steps, for example in the field of construction; Modelling objects in three dimensions usually involves the construction of a mesh which is really just another type of graph; The available moves in a strategy game such as chess; Or the possible scenarios in a computer generated simulation.
Arguably, the graph is one if the most versatile data structures in the field of software engineering.
- Navigation systems
- Web pages links
- Data transmission
- Social networks
- Fluid dynamics
- Critical path analysis
- 3D modelling
- Games and simulations
Terminology
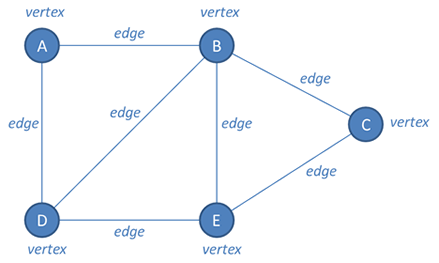
A graph is a collection of interconnected nodes, but unlike a tree, there are no rules about how these nodes can be connected. There is no such thing as a root node, nor are there such things as parent nodes or child nodes. In a graph, a node is more correctly known as a vertex, and vertices are connected by edges.
Typically, a graph will have more edges than vertices. A graph with lots of edges in relation to the number of vertices is said to be dense, while a graph with few edges in relation to the number of vertices is said to be sparse.
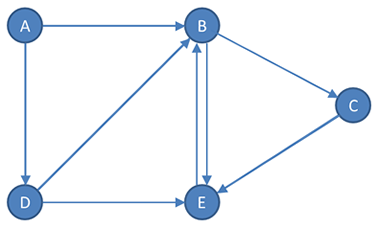
In some graphs the edges are directional. This is known as a directional graph or, sometimes, as a digraph.
A graph in which the edges are not directional is known as an undirected graph, or an unordered graph.
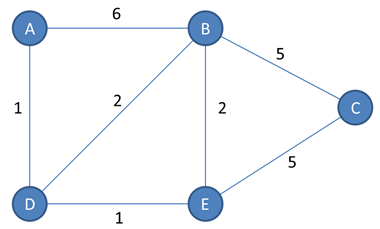
Each edge in a graph can have a weight associated with it. The weight of each edge is also sometimes referred to as the cost. What each cost represents depends of course on the application, for example each cost could be a speed limit, the diameter of a water pipe, or the number of hours to complete a phase of a project.
Note that for a directed graph, there may be two edges between a given pair of vertices, and each could have a different weight.
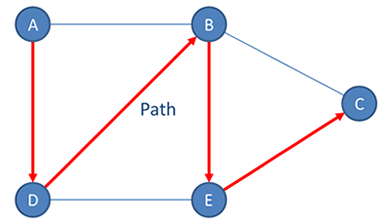
A path is a sequence of vertices in a graph. A graph is said to be connected if there is a path from every vertex to every other vertex.
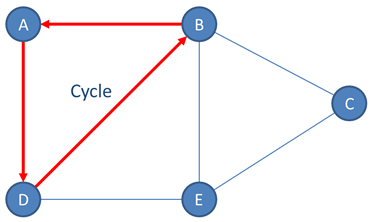
A cycle is a path in which the starting vertex is also the ending vertex.
A tree is a special type of graph, which includes a path from some starting node (the root) to every other node, but a tree has no cycles.