Dijkstra’s algorithm will find the shortest path from one vertex in a graph to another.  In fact, Dijkstra’s algorithm is designed to find the shortest path from a given vertex to ever other vertex in the graph.

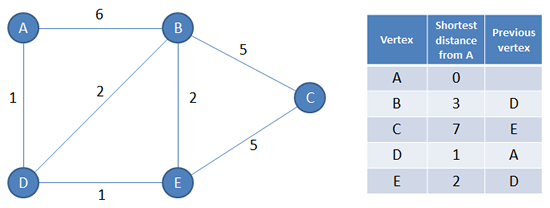
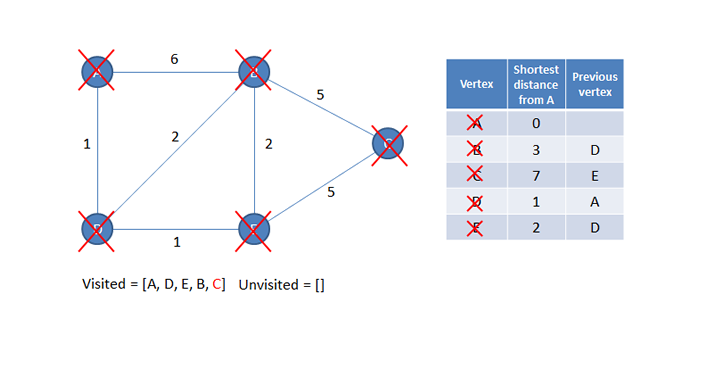
The algorithm will generate a ‘table’ of information as shown here.  This information includes the shortest distance from a starting vertex (in this example, from vertex A) to every other vertex.

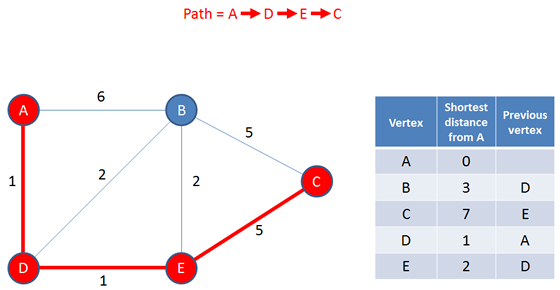
The information generated also includes a list of previous vertices, which indicates each path that was followed from the start to every other. For example, to read off the shortest the path from A to C, examine the table and you can see that the previous vertex for C is E; the previous vertex for E is D, and the previous vertex for D is A.  Hence the shortest path from A to C is A, D, E, C.

 

Generating the path information

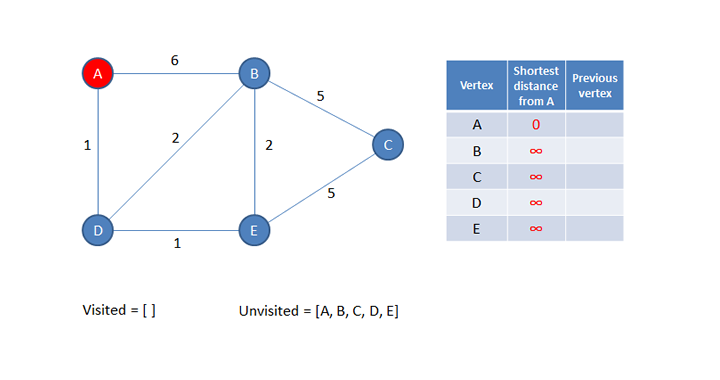
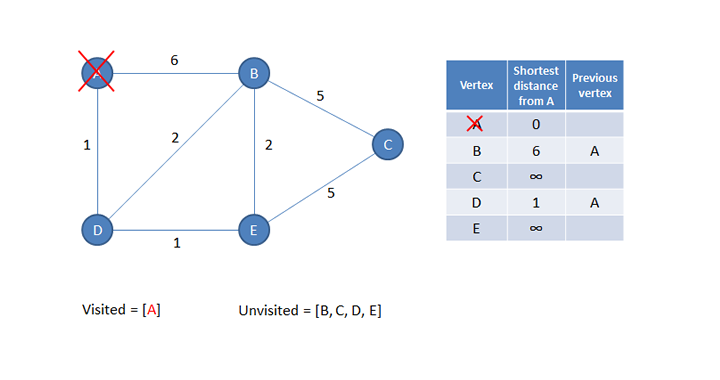
The algorithm begins by making the starting vertex the current vertex.  The distance from the start vertex to the current vertex is written into the table.  This is, of course, zero.  The other distances are currently unknown, so each of these is set to a very large value, namely infinity.

The algorithm also maintains two additional lists.  A list of visited vertices and a list of unvisited vertices.

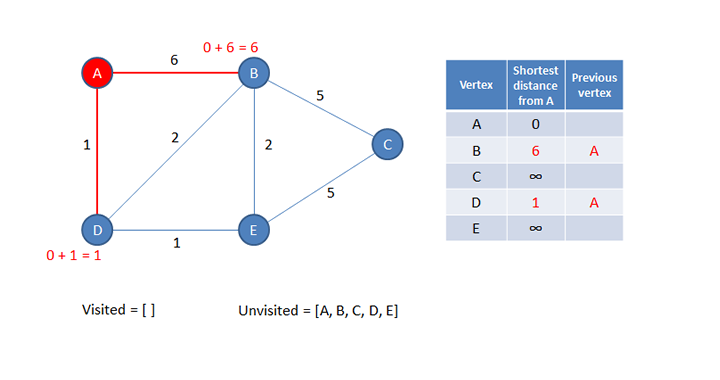
The distance from the current vertex to each of its unvisited neighbours is calculated.  This is done by adding the distance between the start vertex and the current vertex (which is zero at this stage, because the start vertex and the current vertex are one in the same) to the additional distance of each neighbour.  This calculated information is written into the table.  The previous vertex column is also populated with the current vertex for each neighbour.

Now the current vertex is added to the list of visited vertices so that it won’t be considered again.

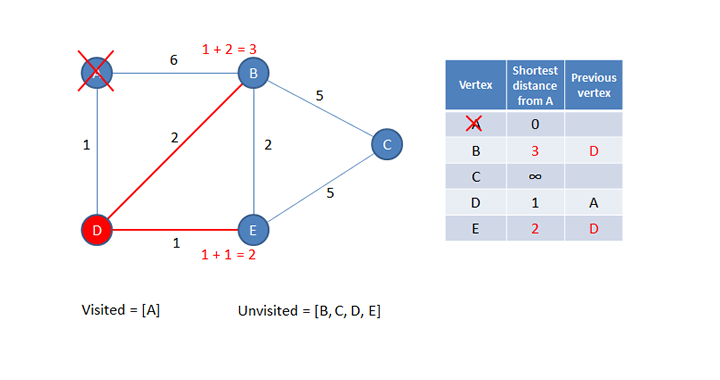
A new current vertex is now selected.  The new current vertex will be the unvisited vertex that is the shortest distance from A.  Looking at the table above, you can see this is D.

The distance from the new current vertex to each of its unvisited neighbours is calculated.  This is done by adding the shortest distance of the current vertex from the start (which can be read from the table) to the additional distance of each neighbour.  This information is then written into the table if the new value is smaller than the existing value.  Notice that the value for B has now been overwritten with a smaller value.  The previous vertex column is also populated with the current vertex for each neighbour.

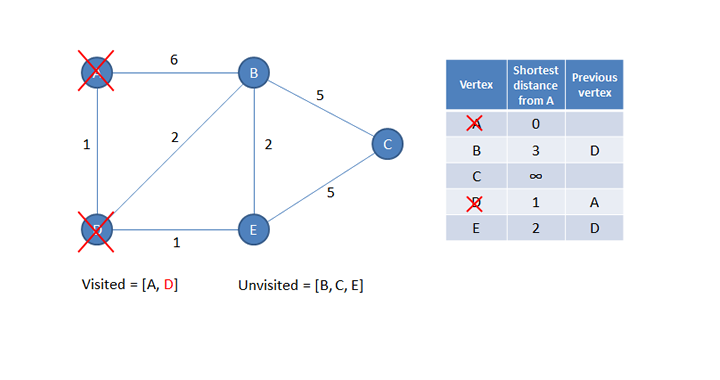
Now the current vertex is added to the list of visited vertices so that it won’t be considered again.

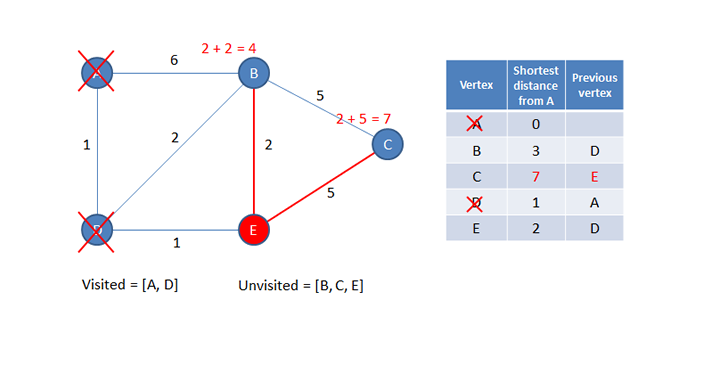
A new current vertex is now selected.  The new current vertex will be the unvisited vertex that is the shortest distance from A.  Looking at the table above, you can see this is E.

The distance from the new current vertex to each of its unvisited neighbours is calculated.  This is done by adding the shortest distance of the current vertex from the start (which can be read from the table) to the additional distance of each neighbour.  This information is then written into the table if the new value is smaller than the existing value.  Notice that the existing value for B in the table has not been replaced because the newly calculated value is larger, nor has the previous vertex for B been replaced.  The value for C is however smaller than its current value of infinity.  The previous vertex column for C is also populated with the current vertex.

Now the current vertex is added to the list of visited vertices so that it won’t be considered again.

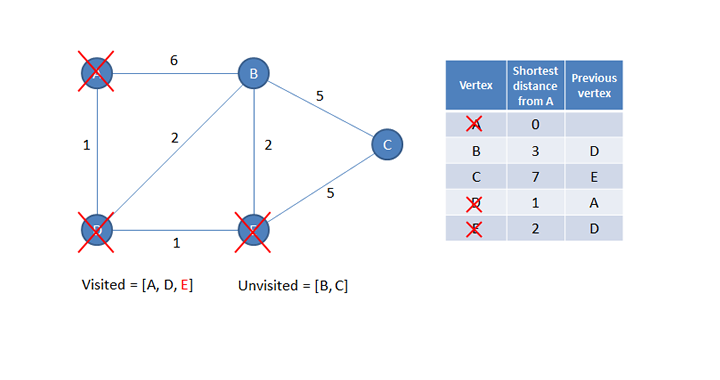
A new current vertex is now selected.  The new current vertex will be the unvisited vertex that is the shortest distance from A.  Looking at the table above, you can see this is B.

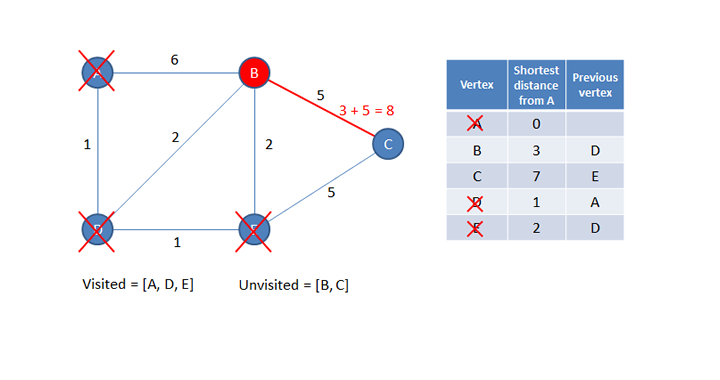
The distance from the new current vertex to each of its unvisited neighbours is calculated.  This is done by adding the shortest distance of the current vertex from the start (which can be read from the table) to the additional distance of each neighbour.  This information is then written into the table if the new value is smaller than the existing value.  Notice that the existing value for C in the table has not been replaced because the newly calculated value is larger.  The previous vertex column for C also remains unchanged.

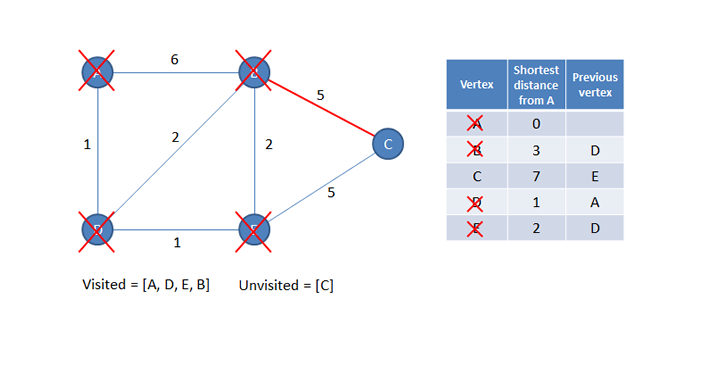
Now the current vertex is added to the list of visited vertices so that it won’t be considered again.

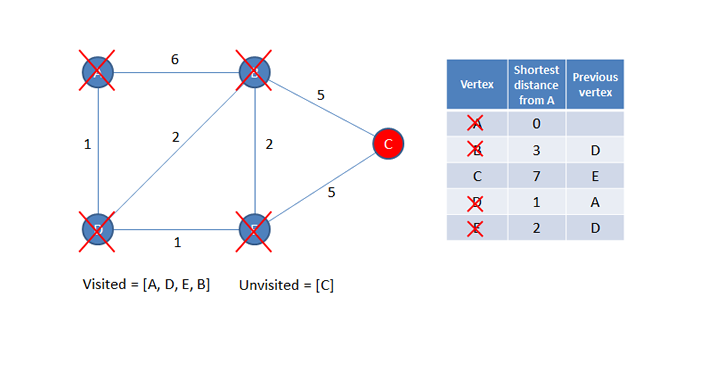
A new current vertex is now selected.  The new current vertex will be the unvisited vertex that is the shortest distance from A.  Looking at the table above, you can see this is C, which is the last remaining unvisited vertex.

Vertex C has no unvisited neighbours so there are no more calculations, and no more updates, to be done.

Now the current vertex is added to the list of visited vertices so that it won’t be considered again.

There are no more unvisited vertices so the algorithm is complete.

Dijkstra’s is a greedy algorithm

The algorithm makes a big assumption whenever it selects a new current vertex.  It assumes that if the closest vertex is chosen, it will ultimately result in the shortest overall path.  To put this another way, the algorithm assumes that choosing a ‘locally optimal’ solution will result in a ‘globally optimal’ solution.  Dijkstra’s algorithm is therefore known as a ‘greedy algorithm’.

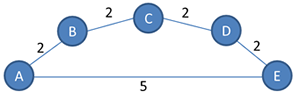
This assumption may not always be correct.  With the graph below, if the starting vertex is A, the next current vertex to be chosen after A would be B, because it is closer than E.  The algorithm would then go on to conclude that the shortest path from A to E is via B, C and D.

 

The algorithm in words

The algorithm described above can be expressed in words as follows:
Let distance of start vertex from start vertex = 0
Let distance of all other vertices from start = ? (infinity)
WHILE vertices remain unvisited
    Visit the unvisited vertex with smallest known distance from start (call this ‘current vertex’)
    FOR each unvisited neighbour of the current vertex
        Calculate the distance from start vertex
        IF the calculated distance of this vertex is less than the known distance
                Update shortest distance to this vertex
                Update the previous vertex with the current vertex
        END IF
    NEXT unvisited neighbour
Add the current vertex o the list of visited vertices
END WHILE