Set notation

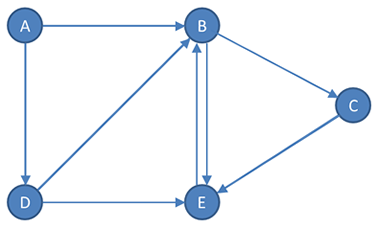
A graph can be described using mathematical set notation.  A graph G is a set of vertices V, and a set of Edges E.  We can list the vertices inside curly brackets, and each edge can be listed as a pair of vertices.

G = (V, E)

V = {A, B, C, D, E}

E = {(A, B), (A, D), (B, C), (B, E), (C, E), (D, B), (D, E), (E, B)}

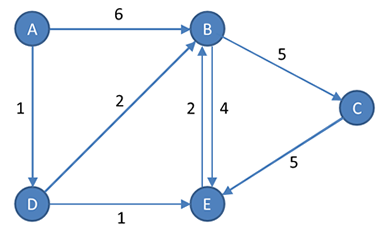
For a weighted directed graph, the cost of each each can be added to this notation.

G = (V, E)

V = {A, B, C, D, E}

E = {(A, B, 6), (A, D, 1), (B, C, 5), (B, E, 4), (C, E, 5), (D, B, 2), (D, E, 1), (E, B, 2)}

So what if we want to code up a graph and work with the data it contains? How do we represent a graph programmatically?
If we take an OO approach to creating a Graph, there are two ways a Graph class could internally maintain the vertices and edges of a graph. These are the adjacency list or the adjacency matrix.

Adjacency list

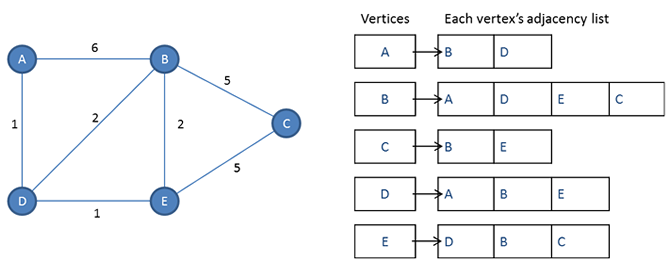
With an adjacency list system, we have a master list of vertices.  Then, for each edge, each starting vertex maintains a list of ending vertices, or, to put it another way, each vertex maintains a list of its neighbours.

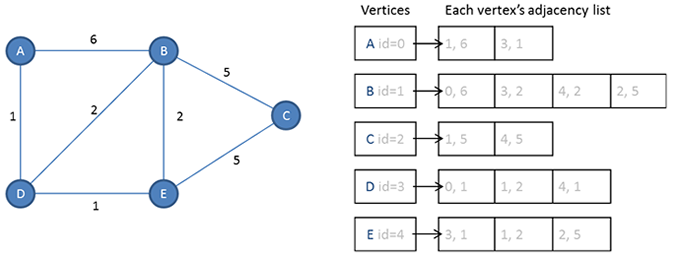
There are several ways an adjacency list could be implemented, but an object oriented approach is probably the most suitable.  We could code up a vertex class, that each vertex object would be instantiated from.  The vertex class would have a property to hold information about a vertex (such as the name of a city if we were representing some kind of map).  Another property could be an identifier for the vertex, and another, an array containing the identifiers of its adjacent vertices.  The master list of vertex objects would also be stored in a simple one dimensional array.

To represent a weighted graph, the cost of each edge could be stored in the adjacency list too.

Using adjacency lists is a very compact, space-efficient, representation of a graph, particularly a sparse graph —you don’t have to store any more data than necessary.  However, determining if a edge exists between two particular vertices would require searching through the adjacency list of one of them.  For a dense graph, the time taken will increases proportionally with the density of the graph.

Adjacency matrix

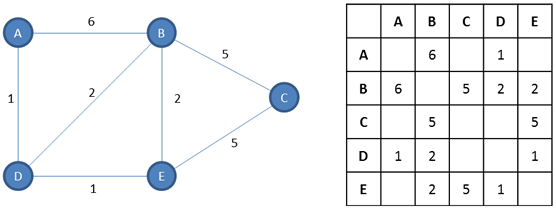
With an adjacency matrix, every vertex is written as a row heading and as a column heading in a grid.

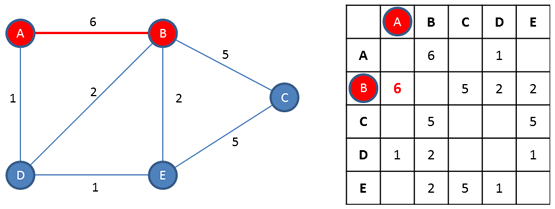
If an edge exists between a pair of vertices, then its weight can be indicated at the intersection of the appropriate row and column.

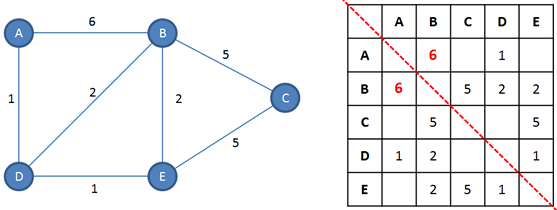
Note that for an undirected graph there is symmetry along the adjacency matrix’s diagonal.  If there is an edge from A to B, there must be a corresponding edge from B to A.  This symmetry would not be present for a directed graph.

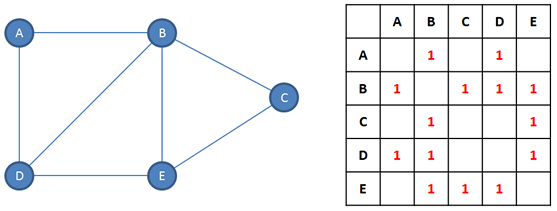
For an unweighted graph, we can simply use a Boolean value to indicate the presence of an edge.

Implementing a graph with an adjacency matrix

An adjacency matrix can be implemented with a two dimensional array. We would still have a vertex class from which we could create each vertex object, but the actual connectivity of the graph would be defined by this 2D array of edges.

One of the advantage of an adjacency matrix over an adjacency list is that determining whether or not an edge exists between two vertices requires a simple array lookup, which takes the same amount of time to do regardless of edge in question.

However an adjacency matrix is not particularly efficient when it comes to space. For a sparse graph much of the adjacency matrix will be empty. Furthermore, for an undirected graph half of the information stored is just duplication.

Which method you choose to use to implement a graph will ultimately depend on the nature of the information it will represent and how you plan to process it.