De Morgan’s theorem provides us with one of the most useful techniques for simplifying some complex Boolean expressions. De Morgan’s theorem states that:
¬(A^B) = ¬Av¬B which reads as NOT (A AND B) = NOT A OR NOT B
and that:
¬(AvB) = ¬A^¬B which reads as NOT (A OR B) = NOT A OR NOT B
De Morgan’s proof
De Morgan’s theorem can be proven by drawing the combination of logic gates for each side of an expression, then working out and comparing their truth tables.
For example, the first De Morgan’s expression:
¬(A^B) = ¬Av¬B
Can also be written as follows:
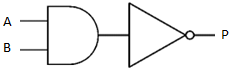 |
= | 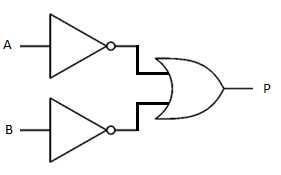 |
Both of these gate combinations share the same truth table.
| A | B | P |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Which means that the logic gate combinations are indeed equivalent.
Similarly, the second De Morgan’s expression:
¬(AvB) = ¬A^¬B
Can also be written as follows:
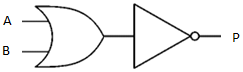 |
= | 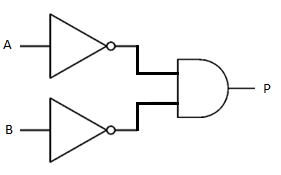 |
Both of these gate combinations share the same truth table.
| A | B | P |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Which means that the logic gate combinations are indeed equivalent.
Simplifying an expression with De Morgan’s
Demorgan’s theorem provides a way to change the operator in an expression from AND to OR, or vice versa. For example, A^B can be expressed as ¬(¬Av¬B)
Given the theorem ¬(A^B) = ¬Av¬B, you can see that all we have done is to NOT each side of the expression.
The process for changing an AND operator to an OR operator can also be thought of as follows:
- Take the original expression A^B, and change the operator from AND to OR so that it reads AvB
- Next, NOT each of the variables in the expression ¬Av¬B
- Finally, NOT the whole expression ¬(¬Av¬B)
Similarly, AvB can be re-written as ¬(¬A^¬B)
The process for changing an OR operator to an AND sign can also be thought of as follows:
- Take the original expression AvB, and change the operator so it reads A^B
- Next, NOT each of the variables ¬A^¬B
- Finally, not the whole expression ¬(¬A^¬B)
Example 1
Putting this into practice, using De Morgan’s theorem to simplify the following expression :
P = ¬(¬Av¬(B^A))
We begin by aiming for only one of the gate types, OR or AND. Let’s attempt to change the OR to an AND. Then we must NOT the individual expressions on either side of the operator we have changed, and NOT the whole expression:
P = ¬¬(¬¬A^¬¬(B^A))
Next, we remove any double NOTs
P = (A^(B^A))
The brackets are no longer necessary as the expression is associative
P = A^B^A
According to the rule A^A=A, we can simply this further to…
P = A^A
We could have tackled the same problem in a different way, by taking the original expression P = ¬(¬Av¬(B^A)) and changing the AND to an OR. While this approach would ultimately produce the same result, there may well be more steps involved.
Example 2
Here is another example, using De Morgan’s theorem to simplify the expression:
P = ¬(¬(¬AvB)^A)
Change the AND to an OR, NOT the individual expressions on either side, then NOT the whole expression:
P = ¬¬(¬¬(¬AvB)v¬A)
Next, we remove any double NOTs
P = ((¬AvB)v¬A)
remove superfluous brackets
P = ¬AvBv¬A
According to the rule ¬A?¬A = ¬A, this becomes
P = ¬AvB
