Logic gates, and combinations of gates, can be written as expressions.  Being able to express gate combinations algebraically, is the basis of the discipline known as ‘Boolean algebra’.  Boolean algebraic expressions can be simplified, according to rules, in much the same way that mathematical equations can be simplified.  This is important in the field of circuit design, allowing engineers to come up with the best possible designs for new circuits.

 

Let’s start by looking at how to produce an expression for a given combination of gates, or draw a combination of gates for a given expression.

 

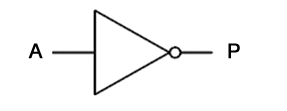
The NOT gate shown here can be expressed as:

P NOT A

 

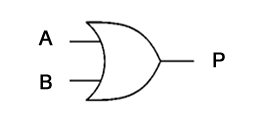
The OR gate shown here can be expressed as:

P = A OR B

 

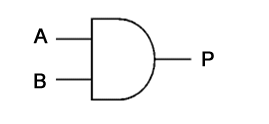
The AND gate shown here can be expressed as:

P = A AND B

 

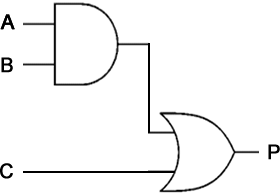
The combination of gates below can be expressed as:

P = (A AND B) OR C

 

Try This – Gate combinations from expressions

Sketch the logic gate combinations that are described by each of the following expressions, where Y is the output and all other letters are inputs:

Y = (A OR B) AND C
Y = (A AND B) OR (C AND D)
Y = NOT((A OR B) AND (C OR D))
Y = NOT(NOT A)

 

Symbols

There are some special symbols that can be used in Boolean expressions in place of the names of the gates. These are as follows:

Gate	Name	Symbol
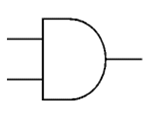	AND	?
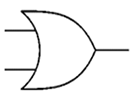	OR	?
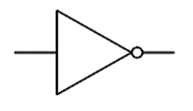	NOT	¬

 

Hence, the following pairs of expressions are equivalent.

P = A OR B	P = A?B
P = A AND B	P = A?B
P = (A AND B) OR C	P = (A?B)?C
P = NOT (A AND B)	P = ¬(A?B)