Public and Private keys

You have seen how the Vigenère Cipher makes use of a keyword to encrypt some plain text. The same keyword is used to decrypt the ciphertext. The keyword is therefore known as a symmetric key.

Asymmetric key encryption relies on two keys, a public key to encrypt data and a private key to decrypt it.

These two keys are mathematically related in such a way that if data is encrypted with the public key, it can only be decrypted with the matching private key.

Logging on to a website

Consider a scenario in which Sally wants to logon to the online retailer Amazon. Sally will be sending all kinds of private information over the Internet including her logon credentials and her bank details.

Before any of this happens, a secure session must be established.

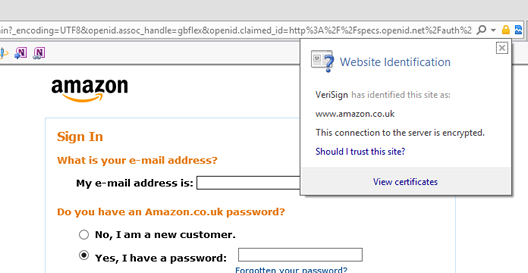
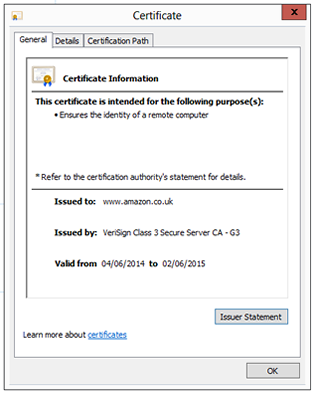
Amazon have already used a key generating algorithm to create a public key and a private key. Anyone can see Amazon’s public key, it is in their digital certificate, which can be viewed by clicking on a padlock in the address bar of most web browsers.

• Sally connects to Amazons website, their public key is sent to her web browser over the Internet
• Sally’s web browser generates a unique symmetric key for the session
• Sally’s web browser encrypts the symmetric key using Amazon’s public key
• The encrypted symmetric key is sent over the Internet to Amazon
• Amazon decrypts the encrypted symmetric key with their private key – only Amazon can do this
• Both Sally’s browser and Amazon know the symmetric key, which is used for all further communication
• Sally logs on securely, and spends lots of money
• The symmetric key is discarded when Sally logs off Amazon’s web site

The RSA Algorithm

The RSA system was invented by Ron Rivest, Adi Shamir, and Leonard Adleman. It is used to generate a public/private key pair used in Asymmetric Key Cryptography.

The RSA algorithm relies on the mathematical properties of prime numbers.

Some integers can be produced by multiplying two prime numbers together. It turns out that each of these ‘sepcial’ integers has a unique prime factorization. For example, the only two prime numbers that will produce 33 when multiplied together are 3 and 11.

If you multiply two very large prime numbers together, you will produce a very large integer, which could only have been produced by a particular pair of primes. Trying to work out which pair of prime numbers were used to produce this integer is an extremely difficult mathematical task.

Without going into the mathematical details, when two large prime numbers have been selected, they can be used to generate two mathematically related keys (each of which is actually a set of numbers). One key can be used to encrypt a message, and only the related key can be used to decrypt it.