The bubble sort, also known as the ripple sort, is one of the least efficient sorting algorithms. However, it is probably the simplest to understand. At each step, if two adjacent elements of a list are not in order, they will be swapped. Thus, larger elements will “bubble” to the end, (or smaller elements will be “bubbled” to the front, depending on implementation) and hence the name.
The principle of a bubble sort is illustrated below: Compare the first two values and swap if necessary. Then compare the next pair of values and swap if necessary. This process is repeated n-1 times, where n is the number of values being sorted.
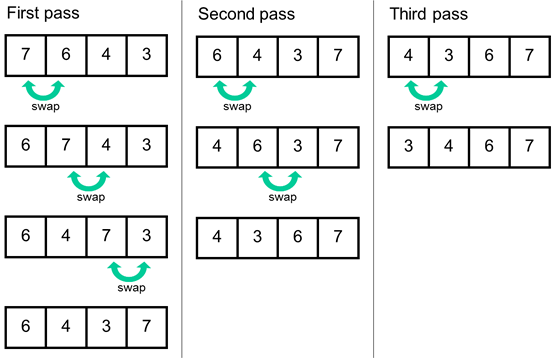
The example above sorts 4 numbers into ascending numerical order. As you can see, this requires 3 (n-1) passes to achieve since there are 4 items of data. The bigger numbers can be seen to bubble (or ripple) to the top.
Algorithm
Repeat as many times as there are items in the list
Repeat for each success pair of elements
If this element > next element then swap elements
Pseudocode
WHILE passes < n-1
WHILE i < n-1
IF item(i) > item(i + 1)
swap items
END IF
i = i + 1
END WHILE
passes = passes + 1
END WHILE
This is not particularly efficient since the process will continue even if the data is already in the correct order. Needless to say there is scope to improve the basic algorithm.
Efficiency of the bubble sort
Consider these questions about how long a bubble sort would take for a given list of items: What is the worst case scenario (what ‘unsorted’ order would require the most comparisons and swaps)? For a list of 5 items (worst case scenario), what is the number of separate operations (comparisons and swaps) required? If there were twice as many items in the list (10), what is the number of separate operations (comparisons and swaps) required? In fact, the bubble sort is one of the least efficient sorting algorithms. If the number of elements to be sorted doubles, the number of swaps is quadrupled. It is said to have ‘quadratic’ time complexity and this can be written as T(n) = O(n2).
