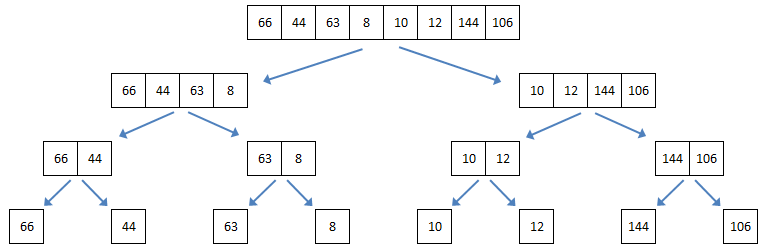
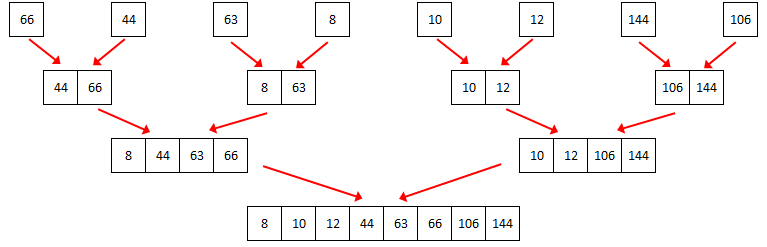
The principle of the merge sort is actually pretty easy to understand. Take a list and split it into two, repeatedly, until you have several lists, each of only item. If a list contains only 1 item, then by definition, it is a sorted list. Then, merge pairs of lists back together, sorting as you go.
Split list successively
Merge pairs of ordered lists
Towards a merge sort implementation
To write a merge sort program, you need three pieces of functionality. Firstly, you need to be able to split a list into two, secondly, you need to be able to merge a pair of ordered list together, sorting as you go, thirdly, you need a program to call the other two, successively in the correct order.
Splitting a List
The following pseudocode shows how one unordered list can be split into two separate unordered lists. The program has to work with a list of any size, so the upper bound of the array we want to split is used to calculate its mid-point. The pointer variable Ptr is used to scan the source array and the first target array (the left hand side target) inside the same loop. A second pointer Ptr2 is used to scan the second target array (the right hand side target). Notice how Ptr2 is set to 0 before the second loop begins, but Ptr continues to grow after the first loop ends.
Middle = (UBound(SourceArray)) / 2
REPEAT
ArrLeft(Ptr) = SourceArray(Ptr)
Ptr = Ptr + 1
UNTIL Ptr = Middle
Ptr2 = 0
REPEAT
ArrRight(Ptr2) = SourceArray(Ptr)
Ptr = Ptr + 1
Ptr2 = Ptr2 + 1
Until Ptr = Ubound(SourceArray)
Merging a pair of ordered lists
The following pseudocode shows how two ordered lists can be merged into one. The two source arrays are Arr1 and Arr2, and the target array is Arr3. Implementation code would first calculate the size of the target by adding together the sizes of the two source arrays. The first loop uses a pair of pointers, Ptr1 and Ptr2 to scan the source lists simultaneously, comparing pairs of values as it goes and copying the smallest to the target. A third pointer Ptr3 scans the targer. If a value is copied from one of the source list pointers, then only that source list pointer is advanced. The target pointer advances unconditionally. Eventually one of the source lists will be exhausted and remaining items from the other source list can be copied to the target unconditionally, since they are already in the correct order. That is the job of one of the other two loops.
REPEAT
IF Arr1(Ptr1) < Arr2(Ptr2) THEN
Arr3(Ptr3) = Arr1(Ptr1)
Ptr1 = Ptr1 + 1
ELSE
Arr3(Ptr3) = Arr2(Ptr2)
Ptr2 = Ptr2 + 1
END IF
Ptr3 = Ptr3 + 1
UNTIL Ptr3 = UBound(Arr1) + UBound(Arr2) + 1
IF Ptr1 <= UBound(Arr1) THEN
REPEAT
Arr3(Ptr3) = Arr1(Ptr1)
Ptr1 = Ptr1 + 1
Ptr3 = Ptr3 + 1
UNTIL Ptr3 = UBound(Arr3) + 1
ELSEIF Ptr2 <= UBound(Arr2) THEN
REPEAT
Arr3(Ptr3) = Arr2(Ptr2)
Ptr2 = Ptr2 + 1
Ptr3 = Ptr3 + 1
UNTIL Ptr3 = UBound(Arr3) + 1
END IF
Putting the merge sort together
Now that we have the building blocks of a merge sort, we can start to put them together. Here’s some pseudocode for a recursive merge sort function. This function has the name MergeSort. It takes one parameter, an array that needs to be sorted. The merge sort function calls two different helper programs, a procedure with the name SplitList and a function with the name MergeTwoLists. This MergeSort function also calls itself.
Because SplitList generates two arrays from one, it needs to be implemented as a procedure rather than a function, because a function cannot return multiple values. The empty arrays ArrLeftHalf and ArrRightHalf can be passed to SplitList by reference, so that once populated, SplitList’s caller can get a hold of them. Notice that after the call to SplitList, MergeSort calls itself passing in the left hand side of the list. This means that before anything else happens, SplitList is called again, to operate on the left hand side of the list. Then, immediately after the call to SplitList, MergeSort calls itself passing in the left hand side of the list.
Function MergeSort(Arr)
Call SplitList(Arr, ArrLeftHalf, ArrRightHalf)
ArrLeftHalf = MergeSort(ArrLeftHalf)
ArrRightHalf = MergeSort(ArrRightHalf)
Return MergeTwoLists(ArrLeftHalf, ArrRightHalf)
End Function
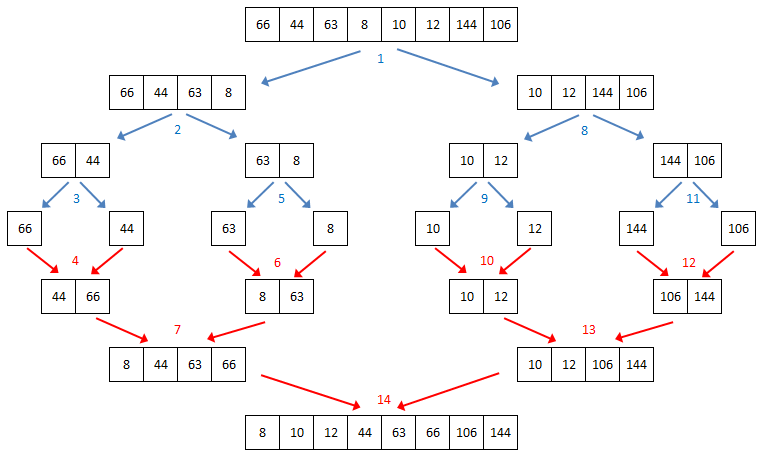
If you think about it, you will see that splitting and merging operations are not performed in the order suggested by the original diagrams above. Examine the diagram below; the numbers indicate the order of operations. The original list is split onto two first, then the left hand side of the original list is split into two, then the left hand side is split again. Once the left hand side has been split as far as it can be, the merging begins, so the fourth operation is to merge the values 44 and 66. The basic rule here is that the list is split if it can be, but merged as soon as possible.