Quick sort is substantially faster than any other sorting method in typical applications. Quick sort uses a divide and conquer strategy for sorting. The basic principle for sorting an array of numbers is this:

Select a value from the array which we will call the pivot value. Any value at all will do.

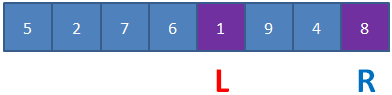
5   2   7   6   1   9   4   8

We will make the first value, 5, the pivot.

Put all of the values less then the pivot on the left, and all of the values larger than the pivot on the right.

4   2   1   5   6   9   7   8

We now have three sub-lists, otherwise known as partitions.  The number 5 is in a sub-list of only one item. Everything smaller than 5 is in a sub-list on its left, and everything bigger than 5 is in a sub-list on its right.  This means that the number 5 is in the correct position, so the number 5 is sorted!

Now we can do the same again to each partition containing more than one value, and then again and again, until we have everything in order.  You may have realised that this is a recursive approach, because we are solving smaller and smaller versions of the same problem.

REPEAT for each partition with > 1 item    
        Partition the list
UNTIL all partitions contain only 1 item

Of the course the clever bit is coming up with a systematic way of getting to three sub-lists as shown above. Only then can we write a program to do this. Let’s play with some cards…

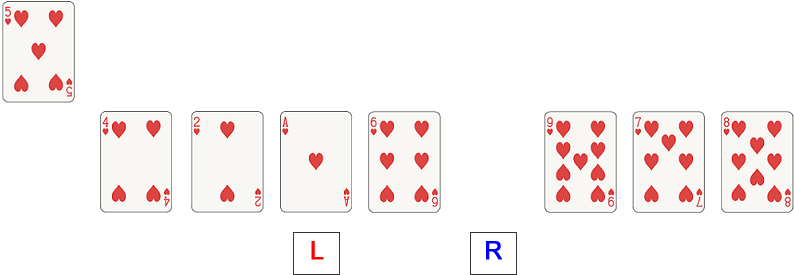
Performing a quick sort

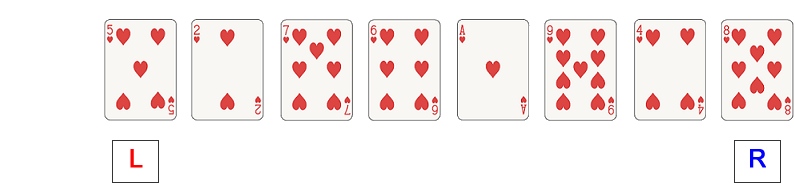
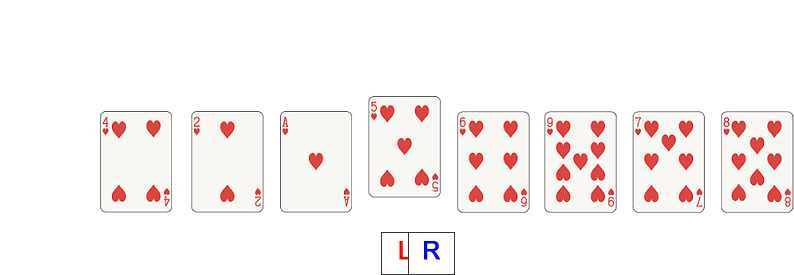
Lay out the cards shown below in front of you (they can be any suit, but use these numbers to start with). Use scrap pieces of paper for a left and a right pointer.

Choose the first card in the list, 5, as a pivot value and move it to one side. There is now a vacant position at the left pointer.

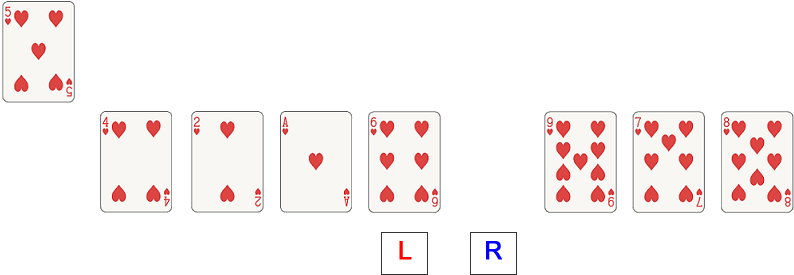
Examine the value at the right pointer. 8 is bigger than 5 so it can stay where it is. Move the right pointer towards the centre.

Examine the value at the right pointer. 4 is less than 5 so move it to the left pointer (leaving a vacant position at the right pointer).

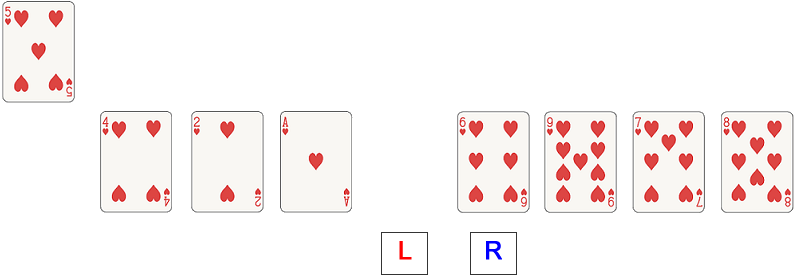
Move the left pointer towards the centre.

Examine the value at the left pointer. 2 is smaller than 5 so it can stay where it is. Move the left pointer towards the centre.

Examine the value at the left pointer. 7 is bigger than 5 so move it to the right pointer (leaving a vacant position at the left pointer).

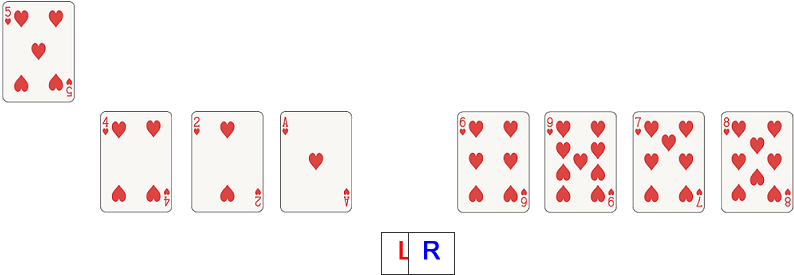
Move the right pointer towards the centre.

Examine the value at the right pointer. 9 is bigger than 5 so it can stay where it is. Move the right pointer towards the centre.

Examine the value at the right pointer. 1 is less than 5 so move it to the left pointer (leaving a vacant position at the right pointer).

Move the left pointer towards the centre.

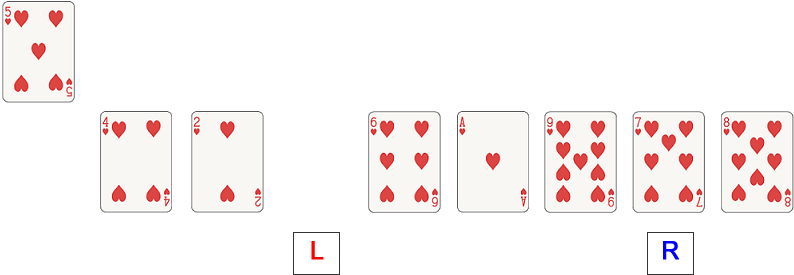
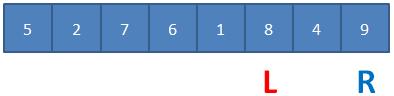
Examine the value at the left pointer. 6 is bigger than 5 so move it to the right pointer (leaving a vacant position at the left pointer).

Move the right pointer towards the centre.

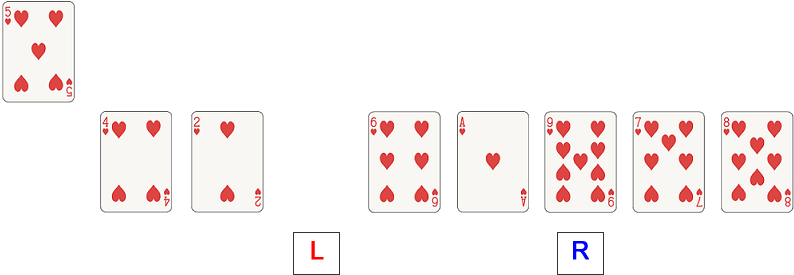
At this stage the pointers collide so we can put the ‘sorted’ pivot value into their position.

We now have three sub-lists. The pivot value is in a sub-list of one item, so it is considered to be sorted. We also have a (potentially) unsorted sub-list of values smaller than 5 on its left, and a (potentially) unsorted sub-list of values larger than 5 on its right.

There were a couple of ‘golden rules’ that you followed to get to this stage. Firstly, you should advance a pointer towards the centre (actually, away from its starting position) and inspect the value at each position, until it is necessary to move a value to the other pointer. Secondly, once a value has been moved to another pointer, then that pointer is the one which should start advancing.

Now take the left hand side sub-list and repeat the whole process again, until this sub-list is sorted. Because there are only three items in this sub-list, you will be able to do this in one pass.

Now take the right hand side sub-list and repeat the whole process again. This will require a couple of recursions to ensure the entire array is sorted.

Do it all again

Take a full set of number cards from 1 to 10 and ask your partner to shuffle them. Use the same technique to sort your cards step by step.

Practice makes perfect.  Shuffle the cards and do it all again.

Pseudocode to partition a list

Here is some pseudocode for a quicksort that employs the algorithm described above.

REPEAT for each partition containing more than 1 item   
        WHILE LeftPointer <> RightPointer
                IF CurrentPointer = “Right” THEN
                        IF Data(RightPointer) < Pivot THEN
                                Data(LeftPointer) = Data(RightPointer)
                                LeftPointer = LeftPointer + 1
                                CurrentPointer = “Left”
                        ELSE
                                RightPointer = RightPointer – 1
                        END IF
                ELSEIF CurrentPointer = “Left” THEN
                        IF Data(LeftPointer) > Pivot THEN
                                Data(RightPointer) = Data(LeftPointer)
                                RightPointer = RightPointer – 1
                                CurrentPointer = “Right”
                        ELSE
                                LeftPointer = LeftPointer + 1
                        END IF
                END IF
        END WHILE
UNTIL all partitions contain only 1 item

 

And here is an alternative way of achieving the same effect:

REPEAT for each partition containing more than 1 item    
        Pivot = Data(LeftPointer)
        WHILE LeftPointer <> RightPointer
                WHILE (Data(RightPointer) > Pivot) And LeftPointer <> RightPointer)
                        RightPointer = RightPointer – 1
                END WHILE
                Data(LeftPointer) = Data(RightPointer)
                WHILE (Data(LeftPointer) < Pivot) And LeftPointer <> RightPointer)
                        LeftPointer = LeftPointer + 1
                END WHILE
               Data(RightPointer) = Data(LeftPointer)
        END WHILE
        Data(LeftPointer) = Pivot
UNTIL all partitions contain only 1 item

Partition a list – alternative method

The algorithm to partition a list described above relies on the explicit selection of a pivot value. The leftmost item in the list is chosen to be the pivot, then items at left and right pointers are compared with the pivot and data is moved from one pointer to the other accordingly.

In this alternative method, we still have a left and a right pointer, but we do not explicitly nominate a pivot value. The principle is to compare items at the pointers and, if necessary, swap them, so that the smaller of the two items is at the left pointer and the larger of the two is at the right pointer.

The process is illustrated here:

Left and right pointers are assigned to the lower and upper bounds of the array.  The values at the left and right pointers are compared.

The value at the left pointer is found to be smaller than the value at the right pointer so they stay where they are and the left pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be smaller than the value at the right pointer so they stay where they are and the left pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be smaller than the value at the right pointer so they stay where they are and the left pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be smaller than the value at the right pointer so they stay where they are and the left pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be smaller than the value at the right pointer so they stay where they are and the left pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be bigger than the value at the right pointer so the values at the left and right pointers are swapped.

The right pointer advances.

The values at the left and right pointers are compared.  The value at the left pointer is found to be bigger than the value at the right pointer so the values at the left and right pointers are swapped.

The left pointer advances.  The pointers collide so the partitioning process is complete.

Notice that when this partitioning process is complete, it is the value that started at the right hand side of the list that ultimately found itself in the correct position; all of the values to the left of 8 are smaller than 8, and all of the values to the right of 8 are larger than 8. In other words, although not explicitly to begin with, the rightmost value is actually the pivot when this method is used to partition a list.

Alternative pseudocode to partition a list

Here  is some pseudocode to partition a list using  the alternative method described above.

WHILE LeftPointer <> RightPointer

        WHILE (Data(LeftPointer) < Data(RightPointer)) And (LeftPointer <> RightPointer)
                LeftPointer = LeftPointer + 1
        END WHILE

        Temp = Data(LeftPointer)
        Data(LeftPointer) = Data(RightPointer)
        Data(RightPointer) = Temp

        WHILE (Data(LeftPointer) < Data(RightPointer)) And (LeftPointer <> RightPointer)
                RightPointer = RightPointer – 1
        END WHILE

        Temp = Data(LeftPointer)
        Data(LeftPointer) = Data(RightPointer)
        Data(RightPointer) = Temp

END WHILE

Recursive quicksort

To perform a quicksort, the partitioning functionality needs to be called repeatedly, for each new partition that is generated which contains more than one item.  Below is a recursive procedure that will do this job.

Sub QuickSort(Data(), Left, Right)

        If Left < Right Then
                PivotPosition = Partition(Data, Left, Right)
                QuickSort(Data, Left, PivotPosition – 1)
                QuickSort(Data, PivotPosition + 1, Right)
        End If

End Sub

This procedure is passed 3 parameters when it is first invoked by another program. These are the array that needs to be sorted, along with the lower and upper bounds of that array. The lower and upper bounds are taken to be the starting positions of the left and right pointers. The data array will need to be passed to it by reference, so it can be accessed by the caller once it has been sorted.

The program focuses on the left hand side first. That is, if it generates a sub-list of more than one item on the left, it will partition this next. When there’s nothing left to process on the left hand side, the program will turn its attention to the most recent right hand side sub-list that it created. This may then generate more left hand side sub-lists, which will then take priority.

Once the first invocation is up and running, the left pointer is smaller than the right (for a list of more than one item), so the program continues.

The Partition function not only partitions the list, but also returns the resting position of the pivot value. The resting position of the pivot value can then be used to determine the upper bound of the sub-list on the left hand side, and the lower bound of the sub-list on the right hand side.

Immediately after the original list has been partitioned, QuickSort calls itself for the first time. The second invocation is passed PivotPosition -1 as the third parameter, so this will be taken to be the value of the right pointer by the next invocation. This means that the second invocation is now working on the left hand side sub-list. The first invocation is suspended, below it on the stack. Each invocation has its own left and right pointer values which are stored in its own stack frame on the call stack. This allows an earlier invocation to pick up from where it left off when it eventually regains control.

When an earlier invocation of QuickSort regains control and finds itself at the top of stack once again, and it can pick up from where it left off. If there is a sub-list to the right of the PivotPosition that this invocation was working with, it may need to be partitioned further. This invocation of QuickSort will therefore call itself again, but this time PivotPostion + 1 is passed in, as the left pointer.

Normally, a call to the Partition function would be expected to generate 3 sub-lists, but sometimes it will generate only two, one of them being the pivot value. If a situation arises in which there is no sub-list on one side of the pivot, the invocation of QuickSort that is called upon to process the absent sub-list will finish without calling the Partition function again. The values of the pointers will indicate that this should happen; left will not be smaller than right. Sometimes, the Partition function will generate a left or a right sub-list that contains only one item. Again, the invocation of QuickSort that is called upon to process a single item sub-list will also finish without calling the Partition function again because left will not be smaller than right.